AI入门笔记-神经网络和深度学习

深度学习概论

备注:常用词

logistic回归=逻辑回归=线性拟合

cost=误差=成本

1.1监督学习

数据类型	网络类型	应用例子
线性数据	价格预测，广告预测	标准网络
图像数据	Convolutional NN(CNN)	图像处理
序列数据	RNN	音频、翻译
图像等	混合网络	自动驾驶

神经网络基础

2.1线性拟合

类似于机器学习的函数y=wx+b,有

$$ \hat{y} = \sigma (wx+b) \text {，输出函数} $$
$$ \sigma(z) = \frac{1}{1+e^{-z}} \text {，Sigmod函数} $$
函数图形类似arctanx,左边趋近于0，右边趋近于1
保证函数wx+b计算出的值（可能性）在有效区间(0-1)

2.2,2.3线性拟合误差函数

$$ L(\hat{y},y)\text{，损失（误差）函数}$$
损失(Loss)函数，用来衡量输出值与真值的差，需要自己定义。
可用方法如平方差，但平方差但对梯度下降不友好。
线性拟合中例子中使用的误差函数
$$ L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y})\text{，误差函数}$$
代价（Cost）函数是对误差函数L求和
$$ J(L)=\frac{1}{m}\sum_{i=0}^m{L…}\text{，误差函数}$$
对J(L)进行梯度下降保证获得全局最优解

2.4梯度下降

重复

$$w:=w-\frac{dJ(w)}{dw}$$
以获得极值
对于多元函数，使用偏导数

微积分及其算例（略）

计算图及其算例

阐述了复合函数求偏导规则(细则略)

2.9在线性拟合中的梯度下降

回顾之前的线性拟合知识
如下公式是前向传播的内容
$$w_1,x_1,w_2,x_2,b->z=w_1x_1+w_2x_2+b->a=\sigma(a)->L(a,y)$$
对L进行偏微分得到w和b所需变化量的过程称为后向传播(back propagation)
接下来讲解m样本整体的训练集,而不是单一的样本.

2.10多样本梯度下降

#意思意思,不严谨的
#严谨的难打
J=0,dw1=0,dw2=0,db=0
for i=1 to m
    zi=w^t*x^i+b
    ---
    for j=0
        dz=a^(j)-y^(j)
    for j=0
        dw1+=x1^(j)dz^(j)
    ...
J/=m
dW1/=m
dw2/=m
db/=m

$$w_1=w_1-\alpha d_1\text{,学习率α对应变化速度}$$

2.11 向量化

用矩阵方法加速计算
课程例子快了300倍

2.12 向量化应用

将2.10中的for嵌套简化为单层

2.13 偏导向量化

正向传播

$$z_i=w^{T}x^{(i)}+b$$
$$z=[z_1\ z_2\ z_3\ z_4\ z_5\ …]=w^{T}X+[b\ b\ b\ b\ b\ …]
=[w^{T}x^{i}+b\ \ \ w^{T}x^{i}+b\ \ \ w^{T}x^{i}+b\ \ \ …]$$

得到公式
$$z=np.dot(w.T,x)+b$$
b是1X1的数,计算中python自动拓展维度

2.14 偏导向量化2

$$dz_i=a^{i}-y^{i}$$
$$dz=[dz_1\ dz_2\ dz_3\ dz_4\ dz_5\ …]$$

得到公式
$$db=\frac{1}{m}\sum_{i=1}^{m}dz^{(i)}
=\frac{1}{m}np.sum(dz)$$
$$dw=\frac{1}{m}Xdz^{T}
=\frac{1}{m}
\begin{bmatrix}x_1&x_2&x_3& \cdots\end{bmatrix}
\begin{bmatrix}dz_1\dz_2\dz_3\\vdots\end{bmatrix}$$
b是1X1的数,计算中python自动拓展维度

3 浅层神经网络

3.1 神经网络的表示

一般不把输入层视为一个标准层,约定上称为layer 0

3.3 计算神经网络的输出

$$z=w^{T}x+b$$
$$a=\sigma(z)=sigmoid(z) \text{,激活函数}$$
对于一个

layer 0有3元素
$$x_1,x_2,x_3$$
分别连接到layer 1的4元素
$$(z^{[1]}|a^{1)}),(z^{[2]}|a^{2)}),(z^{[3]}|a^{3)}),(z^{[4]}|a^{4)})$$
layer 1元素全连接到layer 2(输出层)

$$
Z=
\begin{bmatrix}
\vdots&\vdots&\dots&\vdots\
\vdots&\vdots&\dots&\vdots\
Z^{i}&Z^{i}&\dots&Z^{i}
\end{bmatrix}$$

$$
A=
\begin{bmatrix}
\vdots&\vdots&\dots&\vdots\
\vdots&\vdots&\dots&\vdots\
a^{i}&a^{i}&\dots&a^{i}
\end{bmatrix}$$
$$z^{0}\text{,第一个样本,第一个隐藏单元的计算函数,i为隐藏单元,j为样本} $$
$$a^{0}\text{,第一个样本,第一个隐藏单元的激活函数,i为隐藏单元,j为样本} $$

3.6 激活函数

对于隐藏单元,激活函数
$$a=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$$

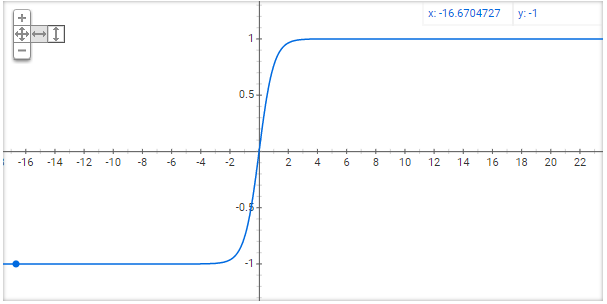
在之后的例子中,除输出层外,均使用tanh更合适.
适用于二元分类输出层.

对于sigmoid和tanh,当z(负)极大时,导数趋近于0.
这时使用线性修正单元ReLU能得到更好的效果,缺点在于负数部分导数为0.

ReLU没有斜率接近0的情况,所以速度快.
虽然对于一半的z,斜率为0,但有足够的隐藏单元使z>0.

对于部分情况,会使用leaky ReLU.
$$a=max(0.01x,x)$$

3.7 使用非线性激活函数的原因

特殊的,有线性激活函数(恒等激活函数)
$$a=z$$

仅将输入特征线性相加后输出,该单元层没有实际作用

因线性函数的组合本身就是线性函数

3.8 激活函数的导数

对于激活函数
$$a=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$$

有导数
$$g’=1-(tanh(z))^2$$

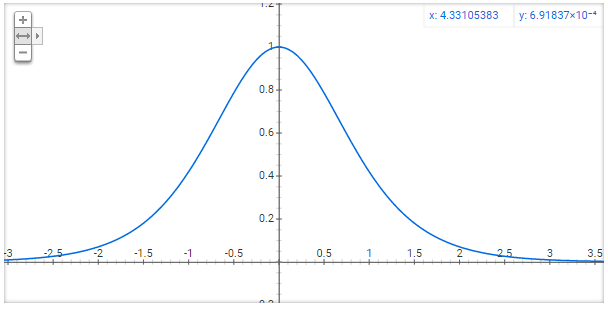
ReLU激活函数

3.9 神经网络的梯度下降法

内容:梯度下降处理单层隐藏神经网络的具体实现并给出重要公式
后续:公式的推导

3:30—5:00不明觉厉
前向公式:
$$Z^{[1]}=W^{[1]}X+b^{[1]}$$

$$A^{[1]}=g^{[1]}(Z^{[1]})$$

$$Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}$$

$$A^{[2]}=g^{[2]}(Z^{[2]})=\sigma(Z^{[2]})$$
反向公式:

$$Y=\begin{bmatrix}y^{[1]}&y^{[2]}&y^{[3]}& \cdots&y^{[m]}\end{bmatrix}$$

$$dZ^{[2]}=A^{[2]}-Y$$

$$dW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T}$$

$$db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=true)$$

$$dZ^{[1]}=W^{[2]T}dZ^{[2]}g^{[1]’}(Z^{[1]})\text 其中号前后均为(n^{[1]},m)矩阵$$
$$dW^{[1]}=\frac{1}{m}dZ^{[1]}X^T$$
$$db^{[1]}=\frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=true) \text 如果n^{[2]}=1,keepdims不作为$$

3.10 （选修）直观理解反向传播

略过

3.11 随机初始化

对于多个隐藏单元,使用0初始化W会导致多个单元进行了相同的计算,重复计算失去意义.
可以使用随机初始化解决.
常用:

np.random.dandn((2,2))*0.01
#对于sigmoid函数,w太大太小会学习缓慢,使用0.01可以加快学习
#深层神经网络会考虑使用其他常数

---

第三周测验错题集

1.以下哪一项是正确的？

• X是一个矩阵，其中每个列都是一个训练示例。
• a^{[2] (12)}表示第二层和第十二层的激活向量。
• a^[2]表示第二层的激活向量。
• a^[2]₄是第二层第四层神经元的激活的输出。

2.tanh激活函数通常比隐藏层单元的sigmoid激活函数效果更好，因为其输出的平均值更接近于零，因此它将数据集中在下一层是更好的选择，请问正确吗？

• True
• False

3.其中哪一个是第m层向前传播的正确向量化实现，其中1≤m≤M(略干扰项)

• Z[m]=W[m]A[m−1]+b[m]
• A[m]=gm

4.您正在构建一个识别黄瓜（y = 1）与西瓜（y = 0）的二元分类器。 你会推荐哪一种激活函数用于输出层？

• ReLU
• Leaky ReLU
• sigmoid
• tanh

5.看一下下面的代码：

A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)

请问B.shape的值是多少?

B.shape = (4, 1)

we use (keepdims = True) to make sure that A.shape is (4,1) and not (4, ). It makes our code more rigorous.

我们使用（keepdims = True）来确保A.shape是（4,1）而不是（4，），它使我们的代码更加严谨。

6.假设你已经建立了一个神经网络。 您决定将权重和偏差初始化为零。 以下哪项陈述是正确的？

• 第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过多次梯度下降迭代后，层中的每个神经元节点都会计算出与其他神经元节点相同的东西。
• 第一个隐藏层中的每个神经元将在第一次迭代中执行相同的计算。 但经过一次梯度下降迭代后，他们将学会计算不同的东西，因为我们已经“破坏了对称性”。
• 第一个隐藏层中的每一个神经元都会计算出相同的东西，但是不同层的神经元会计算不同的东西，因此我们已经完成了“对称破坏”。
• 即使在第一次迭代中，第一个隐藏层的神经元也会执行不同的计算， 他们的参数将以自己的方式不断发展。

7.Logistic回归的权重w应该随机初始化，而不是全零，因为如果初始化为全零，那么逻辑回归将无法学习到有用的决策边界，因为它将无法“破坏对称性”，是正确的吗？

• True
• False
  Logistic Regression doesn’t have a hidden layer. If you initialize the weights to zeros, the first example x fed in the logistic regression will output zero but the derivatives of the Logistic Regression depend on the input x (because there’s no hidden layer) which is not zero. So at the second iteration, the weights values follow x’s distribution and are different from each other if x is not a constant vector.

8.Logistic回归没有隐藏层。 如果将权重初始化为零，则Logistic回归中的第一个示例x将输出零，但Logistic回归的导数取决于不是零的输入x（因为没有隐藏层）。 因此，在第二次迭代中，如果x不是常量向量，则权值遵循x的分布并且彼此不同。

您已经为所有隐藏单元使用tanh激活建立了一个网络。 使用np.random.randn（..，..）* 1000将权重初始化为相对较大的值。 会发生什么？

• 这没关系。只要随机初始化权重，梯度下降不受权重大小的影响。

• 这将导致tanh的输入也非常大，因此导致梯度也变大。因此，您必须将α设置得非常小以防止发散; 这会减慢学习速度。

• 这会导致tanh的输入也非常大，导致单位被“高度激活”，从而加快了学习速度，而权重必须从小数值开始。

• 这将导致tanh的输入也很大，因此导致梯度接近于零， 优化算法将因此变得缓慢。

tanh becomes flat for large values, this leads its gradient to be close to zero. This slows down the optimization algorithm.

tanh对于较大的值变得平坦，这导致其梯度接近于零。 这减慢了优化算法。

9.看一下下面的单隐层神经网络：

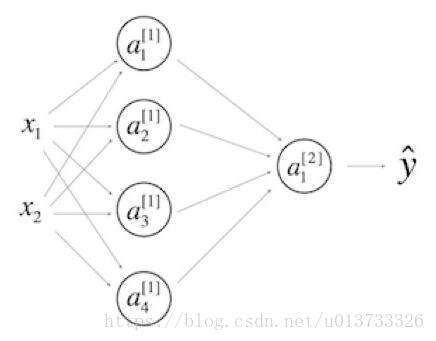
• b[1]b[1] 的维度是(4, 1)
• W[1]W[1] 的维度是 (4, 2)
• W[2]W[2] 的维度是 (1, 4)
• b[2]b[2] 的维度是 (1, 1)
  博主注：我只列出了正确的答案。

请注意: 点击这里 来看一下公式。

10.I在和上一个相同的网络中，z^[1] 和 A^[1]的维度是多少？

• z^[1] 和 A^[1] 的维度都是 (4,m)
  博主注：我只列出了正确的答案。

请注意: 点击这里 来看一下公式

---

第四周 深层神经网络

4.1 深层神经网络

符号约定

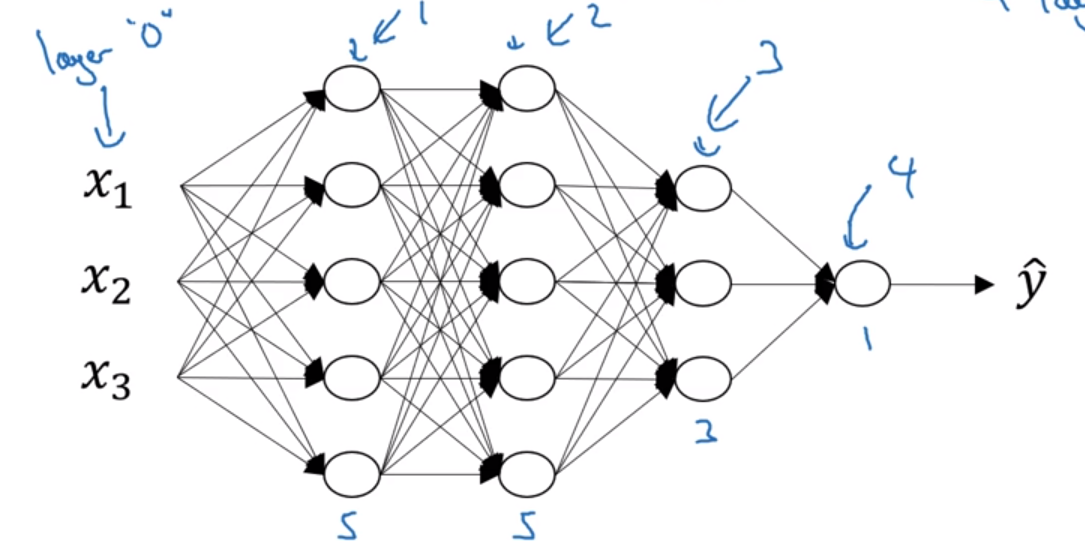
L表示神经网络的层数

n^l 节点数量 或 l上单元数量
a^l 层l的激活函数

输入层:

a⁰ 层l的激活函数

a⁰输入数据

a^L输出数据

n¹=5

$$Z^{[l]}=W^{[l]}X^{[l-1]}+b^{[l]}$$

$$A^{[l]}=g^{[l]}(Z^{[l]})$$

4.2 深层网络中的前向传播

层间计算不能避免使用类for循环计算

4.3 核对矩阵的维数

debug最有效的方法是用纸过一遍算法中矩阵的维数

dZ,dA与Z,A具有相同的维度

4.4 为什么使用深层表示

有的功能在使用浅层网络会需要指数倍数量的隐藏单元来完成计算

对于电路理论,更多的层代表了数据的高位(个十百千/2,4,8,16,32…),如果只使用浅层,将会需要指数级的隐藏单元(2ⁿ)

4.5 搭建深层神经网络块